Return To Contents


CALCULUS 1 PROBLEMS & SOLUTIONS

7.3.2
Finding Volumes By Using Cylindrical Shells


Go To Problems & Solutions


Review


1. Cylindrical Shells

Let f be a continuous function on [a, b] where 0 £ a < b and f(x) ³ 0 for all x in [a, b]. See Fig. 1.
When the plane region R bounded by f, y = 0, x = a, and x = b is revolved about the y-axis, it
generates a solid S, as shown in Fig. 2. We wish to find the volume V of S. If we use the slice method
as discussed in Section 7.3.1 Review Part 4, a typical slice will be perpendicular to the y-axis, the
integration will be along the y-axis, the increment will be dy, and the integrand will be a function of y.
That entails solving the equation y = f(x) for x to get an equation of the form x = g( y). That task may
be easy, hard, or impossible.

So in this section we're going to investigate another approach, one that doesn't require solving the
equation y = f(x) for x. Let x be an arbitrary point in [a, b], as shown in Fig. 1. Erect a thin vertical
rectangle at x and of width dx and height f(x). The rectangle is gray colored. When the region R is
revolved about the y-axis, the vertical line segment at x sweeps out a cylindrical cross section, and
the rectangle sweeps out a cylindrical shell, as shown gray colored in Fig. 2. Note that the
rectangular strip is parallel to the y-axis, which is the axis of revolution, and the cylindrical shell has
its axis along the axis of revolution. Let dV be the volume of the shell. The volume V of the solid S can
be approximated by the sum of the differential volume elements of such shells. Each shell in Fig. 2
corresponds to a rectangle in Fig. 1. The rectangles run from a to b. Thus so do the shells.
Consequently, V is the integral of dV from x = a to x = b. Hence, the integration will be along the
x-axis and the integrand will be a function of x (an expression involving f(x), as is the case for the slice
method; see the volume formula in Section 7.3.1 Review Part 1). This shows that we won't have to
solve the equation y = f(x) for x.

Fig. 1 The colored region is revolved about the y-axis.

Fig. 2 The solid of revolution and a cylindrical shell.

Fig. 3 The cylindrical shell is reproduced here for clarity.

Now let's find the volume V. The cylindrical shell is reproduced in Fig. 3. Its volume dV is:

dV = (surface area of cylinder) . (thickness of shell)
= ((perimeter of base of shell) . (height of shell)) . dx
= ((2p . (radius of base of shell)) . y) . dx
= ((2p . x) . y) . dx
= 2pxf(x) dx.

It follows that the volume V of the solid S is:



For obvious reason, this approach of finding the volume of revolution by using cylindrical shells is called
the method of cylindrical shells, or, for simplicity, the shell method.


Example 1 – The Torus

A solid generated by revolving a disk about an axis which is on its plane and external to it is called a
torus (a doughnut --- Wow, delicious! says Homer Simpson --- Well, a doughnut-shaped solid --- Doh!
... Nuts! ... Hmmm, doughnuts ...). In Section 7.3.1 Problem & Solution 7 we've found the volume of the
torus using the slice method. The torus is reproduced in Fig. 4. Find its volume using the shell method.

Fig. 4 A torus.

Fig. 5 The torus can be generated by revolving this disk about the y-axis.

Remarks 1

i. The shell method gives the same result as does the slice method.

ii. Instead of a rectangle, we simply draw a strip, and call it a rectangle and treat it as such when
finding the volume of the generated cylindrical shell. This is because drawing a strip is simpler than
drawing a rectangle and there's no harm in doing so.

iii. The axis of revolution is the y-axis.

iv. The rectangle is parallel to the axis of revolution.

v. Given a point x in [b – a, b + a], there correspond two points on the circle: (x, y) and (x, – y),
where we assume y ³ 0 by considering only the upper semi-circle. So the height of the rectangle is
y – (– y) = 2y, which we express in terms of x.

vi. The rectangular strip is perpendicular to the x-axis. Thus, the increment is dx. Hence, the
integration is along the x-axis and we must express both the radius and the height of the shell in
terms of x.

Go To Problems & Solutions Return To Top Of Page


2. Axis Of Revolution Is Horizontal And/Or Doesn't Coincide
With A Coordinate Axis

Example 2

In Section 7.3.1 Review Part 5 we used the slice method to find the volume of the solid generated by
revolving the plane region bounded by y = x² and y = 3 about the line y = –1. Now use the shell method
to find that volume.

Solution

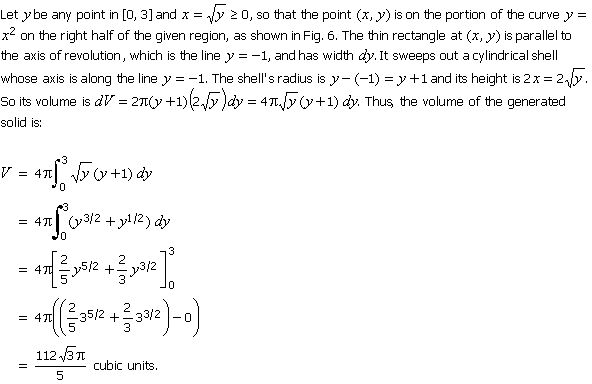
Fig. 6 Plane region bounded by y = x^2 and y = 3 is revolved about line y = –1.

EOS


Remarks 2

i. The shell method gives the same result as does the slice method.

ii. The shell method can also be employed when the axis of revolution doesn't coincide with a
coordinate axis.

iii. The axis of revolution is parallel to the x-axis. The axis of revolution is horizontal, while in the case
for the torus above it's vertical.

iv. The rectangle is parallel to the axis of revolution.

v. Given a point y in [0, 3], there correspond two points on the curve y = x²: (x, y) and (–x, y),
where we assume x ³ 0 by considering only the right half portion of the part of the curve which
bounds the region. So the height of the rectangle is x – (–x) = 2x, which we express in terms of y.

vi. The rectangular strip is perpendicular to the y-axis. Thus, the increment is dy. Hence, the
integration is along the y-axis and we must express both the radius and the height of the shell in
terms of y.

Go To Problems & Solutions Return To Top Of Page


3. General Case

We've seen that the shell method can be used whether the axis of revolution is vertical or horizontal,
and whether it coincides with a coordinate axis or not. In the case where the curve is y = f(x) and the
axis of revolution coincides with the y-axis (and thus is vertical) as discussed in Part 1, the radius and
height of the shell are x and f(x) respectively and the increment is dx. One or more of these aspects
may no longer be true in other cases, as shown for one case in Part 2. However, the basic formula for
the volume element is the same: dV = 2p . (radius of shell) . ( height of shell) . (differential increment).
Let r and h be the radius and height of the shell respectively. Thus, in general:



Return To Top Of Page



Problems & Solutions

1. Use the shell method to find the volume of the solid generated by revolving the plane region
bounded by y = x², y = 9, and x = 0 about the y-axis.

Solution

Let x be an arbitrary point in [0, 3]. The vertical rectangle at x and of width dx sweeps out a cylindrical
shell with radius x and height 9 – x². So its volume is dV = 2px(9 – x²) dx. Consequently, the volume
of the solid is:

Note

The volume of this solid was also found in Section 7.3.1 Review Part 4 using the slice method. For this
solid, the slice and shell methods require roughly the same amount of work.

Return To Top Of Page





Solution





Note

The volume of this solid with a hole was also found in Section 7.3.1 Review Part 3 using the slice
method. There, we had to take the hole into consideration in calculating the volume of the washer slice.
Here, using the shell method, the hole has no role in our calculation of the volume of the shell.

Return To Top Of Page



3. Utilize the shell method to find the volume of the solid generated by revolving the triangular region
bounded by y = x, y = 0, and x = 2 about the line x = 3.

Solution



Let x be an arbitrary point in [0, 2]. So the point (x, y) where y = x is on the line y = x. The vertical
rectangle at x and of width dx sweeps out a cylindrical shell with radius 3 – x and height y = x. Thus,
the volume of the shell is dV = 2p(3 – x)x dx. It follows that the volume of the solid is:



Return To Top Of Page



4. The plane region bounded by x = y² and y = – x + 2 is revolved about the line y = 1. Find the
volume of the generated solid by using the shell method.

Solution



The points of intersection of x = y² and y = – x + 2 are (x, y) where x = y² and y = – x + 2, so
y² + y – 2 = 0, thus ( y – 1)( y + 2) = 0, hence y = 1 or –2. Therefore, the points are (1, 1) and (4, –2).
Let y be any point in [–2, 1]. The horizontal rectangle at y and of width dy sweeps out a cylindrical
shell. From y = – x + 2 we get x = – y + 2. So the volume of the shell is dV =
2p(1 – y)((– y + 2) – y²) dy = 2p( y³ – 3y + 2) dy. Thus, the volume of the solid is:



Note

The volume of this solid was also found in Section 7.3.1 Problem & Solution 5 using the slice method.
For this solid, the shell method is simpler than the slice method.

Return To Top Of Page



5. Find the volume of the solid generated by revolving the plane region bounded by y = e^x, y = 0, x =
0, and x = 1 about the y-axis.

Solution



Let x be an arbitrary point in [0, 1]. The vertical rectangle at x and of width dx describes a cylindrical
shell whose volume is dV = 2pxe^x dx. Therefore, the volume of the solid is:



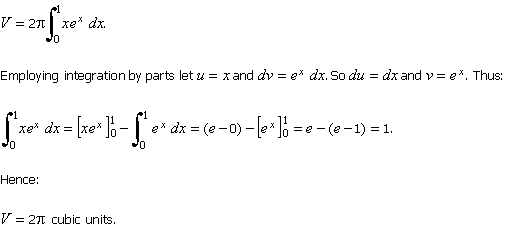
Return To Top Of Page Return To Contents